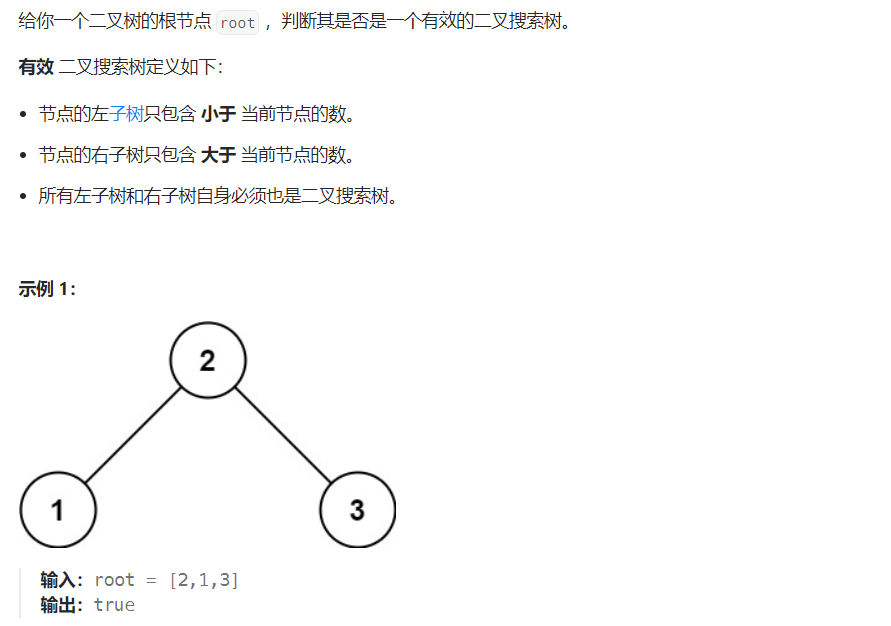
98. 验证二叉搜索树
解法一:递归
验证搜索树可以转换为每一颗子树的 小 < 本身 < 大 的思想。
根节点由于没有限制,只要满足 -inf - +inf 即可以,
然后随着左右子树的递归遍历,分别改变上界和下界。
如左子树必须满足 (-inf, root.val),右子树:(root.val, +inf)。
1
2
3
4
5
6
7
8
9
10
| class Solution {
public boolean isValidBST(TreeNode root) {
return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
}
public boolean isValidBST(TreeNode root, long left, long right){
if(root == null) return true;
if(root.val >= right || root.val <= left) return false;
return isValidBST(root.left, left, root.val) && isValidBST(root.right, root.val, right);
}
}
|
解法二:中序遍历
由于二叉搜索树的中序遍历得到的一定是有序的数组。
只要判断中序遍历过程中,是否有序即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public boolean isValidBST(TreeNode root) {
long min = Long.MIN_VALUE;
Deque<TreeNode> stack = new ArrayDeque<>();
while(!stack.isEmpty() || root != null) {
while(root != null){
stack.push(root);
root = root.left;
}
root = stack.pop();
if(root.val <= min) return false;
min = root.val;
root = root.right;
}
return true;
}
}
|
模仿递归的一个关键因素是保证状态始终在 root 上变化。
230. 二叉搜索树中第K小的元素
最简单的思路就是:中序遍历,然后返回第 k-1 个元素。
迭代实现,不需要访问所有元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public int kthSmallest(TreeNode root, int k) {
Deque<TreeNode> stack = new ArrayDeque<TreeNode>();
while (root != null || !stack.isEmpty()) {
while (root != null) {
stack.push(root);
root = root.left;
}
root = stack.pop();
--k;
if (k == 0) {
break;
}
root = root.right;
}
return root.val;
}
}
|
记录子树的结点数
之所以需要中序遍历前 k 个元素,是因为不知道第 k 个元素是在树的什么位置。
也就是不知道子树的结点数量,需要一层一层遍历,然后计数。
所以可以先记录每颗子树的结点数。
那么第 k 小元素的位置一定满足如下条件:
以 node 作为根结点,开始搜索:
如果 node 的左子树的结点数 left < k−1**,则第 k 小的元素一定在 node 的**右子树**中,令 node 等于其的右子结点,将左子树的结点数算在内,然后令 **k 等于 k−left−1**,并继续搜索;
如果 node 的左子树的结点数 **left == k−1**,则**第 k 小的元素即为 node** ,结束搜索并返回 node 即可;
如果 node 的左子树的结点数 **left > k−1,则第 k 小的元素一定在 node 的左子树中,令 node 等于其左子结点,并继续搜索。
为了提高效率,选择将每个子树的结点数存在哈希表中。
递归思想:一颗子树的左右结点数,分别是左右两颗子树的总结点数,只要不断往下遍历就能找到。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| class Solution {
List<Integer> list = new ArrayList<>();
public int kthSmallest(TreeNode root, int k) {
MyBst myBst = new MyBst(root);
return myBst.kthSmallest(k);
}
}
class MyBst {
TreeNode root;
Map<TreeNode, Integer> nodeNum;
public MyBst(TreeNode root){
this.root = root;
this.nodeNum = new HashMap<>();
countNodeNum(root);
}
public int kthSmallest(int k) {
TreeNode node = root;
while(node != null){
int left = nodeNum.getOrDefault(node.left, 0);
if(left < k-1) {
node = node.right;
k -= left+1;
} else if (left == k-1){
break;
} else {
node = node.left;
}
}
return node != null ? node.val : -1;
}
private int countNodeNum(TreeNode node) {
if(node == null) return 0;
nodeNum.put(node, 1+countNodeNum(node.left)+countNodeNum(node.right));
return nodeNum.get(node);
}
}
|
199. 二叉树的右视图
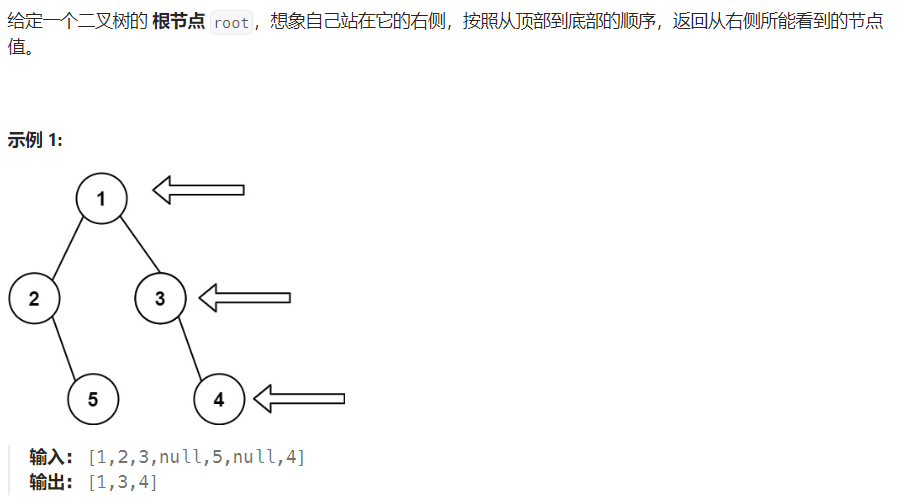
右视图就是从每一层的右边看过去的第一个节点。
由于不知道树的具体结构,所以可以全部遍历然后取【每一层的】右边第一个。
可以用深度优先遍历,每次优先访问最右边的,然后用一个哈希表记录每一层访问到的第一个元素,其它元素直接舍弃。
DPS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| class Solution {
public List<Integer> rightSideView(TreeNode root) {
if(root == null) return Collections.emptyList();
Map<Integer, Integer> map = new HashMap<>();
int max_depth = -1;
Deque<TreeNode> nodeStack = new LinkedList<>();
Deque<Integer> depthStack = new LinkedList<>();
nodeStack.push(root);
depthStack.push(0);
while(!nodeStack.isEmpty()) {
TreeNode node = nodeStack.pop();
int depth = depthStack.pop();
max_depth = Math.max(max_depth, depth);
if(!map.containsKey(max_depth)) map.put(max_depth, node.val);
if(node.left != null) {
nodeStack.push(node.left);
depthStack.push(depth+1);
}
if(node.right != null) {
nodeStack.push(node.right);
depthStack.push(depth+1);
}
}
ArrayList<Integer> ans = new ArrayList<>();
for(int i=0; i<=max_depth; i++)
ans.add(map.get(i));
return ans;
}
}
|
或者用广度优先搜索,每一层的最后一个就是右边第一个。
BFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public List<Integer> rightSideView(TreeNode root) {
if(root == null) return Collections.emptyList();
ArrayList<Integer> ans = new ArrayList<>();
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
while(!q.isEmpty()){
int layerNum = q.size();
for(int i=0; i<layerNum; i++){
TreeNode node = q.poll();
if(i == layerNum-1) ans.add(node.val);
if(node.left != null) q.offer(node.left);
if(node.right != null) q.offer(node.right);
}
}
return ans;
}
}
|
114. 二叉树展开为链表

常规思路可以先按照先序遍历存储一条链表,然后从 root 开始逐一复制节点。
或者直接“拼接”。
只要按照先序遍历的顺序,找到左子树最后一个节点,然后拼接上右子树,
再把左子树整个移到右边去,如此循环处理每一个右节点,最后就变成直直的一条链表了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public void flatten(TreeNode root) {
while(root != null){
if(root.left != null){
TreeNode last_right = root.left;
while(last_right.right != null) {
last_right = last_right.right;
}
last_right.right = root.right;
root.right = root.left;
root.left = null;
root = root.right;
} else{
root = root.right;
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| 1
/ \
2 5
/ \ \
3 4 6
//将 1 的左子树插入到右子树的地方
1
\
2 5
/ \ \
3 4 6
//将原来的右子树接到左子树的最右边节点
1
\
2
/ \
3 4
\
5
\
6
//将 2 的左子树插入到右子树的地方
1
\
2
\
3 4
\
5
\
6
//将原来的右子树接到左子树的最右边节点
1
\
2
\
3
\
4
\
5
\
6
......
|
300. 最长递增子序列

动态规划
定义状态:dp[i] 的值就代表以 nums[i] 结尾的最长子序列长度
转移方程:遍历之前的 dp[j],当 nums[j] < nums[i] 时表示可以接在后面,保留拼接后的最大值 dp[i] = max(dp[i], dp[j]+1)
初始状态:每个数元素本身至少就是一个长度为 1 的序列。
返回值:记录 dp[i] 的最大值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public int lengthOfLIS(int[] nums) {
int n = nums.length;
if(n == 0) return 0;
int[] dp = new int[n];
Arrays.fill(dp, 1);
int res = 0;
for(int i=0; i<n; i++){
for(int j=0; j<i; j++){
if(nums[j] < nums[i]) dp[i] = Math.max(dp[i], dp[j]+1);
}
res = Math.max(res, dp[i]);
}
return res;
}
}
|
动态规划 + 二分法
普通的动态规划需要找到能接到上的最长的子序列,所以是 dp[i] = max(dp[i], dp[j]+1)。
那如果维护一个 tails 数组,不断取出子序列 nums[1,k] 尾部元素更新 tails 数组,只保留更小的尾部,那么 tails 数组的长度就是最终答案。
优化的精髓在于:本身是一个有序序列,能够通过二分法更新 nums[1,k] 的尾部最小值,保证每次迭代都是基于之前子序列的最大可能有序序列。
这个更新尾部最小值,很好的“拿出了”一长串递增序列中的无关元素。
如:
1
2
3
4
5
6
7
| nums: 1 5 3
取出 1
tails: 1
取出 5(能接上)
tails: 1,5
取出 3(替掉5,重新接上)
tails: 1,3
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public int lengthOfLIS(int[] nums) {
int n = nums.length;
int[] tails = new int[n];
int res = 0;
for(int num: nums){
int i=0, j=res;
while(i < j){
int m = (i+j)/2;
if(tails[m] < num) i = m+1;
else j = m;
}
tails[i] = num;
if(res == j) res++;
}
return res;
}
}
|
105. 从前序和中序遍历序列构造二叉树
通过后序和中序、前序和中序都能构造二叉树。
因为可以确定根的位置,然后从中序遍历中,将根的两边分为左右子树。
再不断递归划分左右子树,然后回溯就构建成功了。
前序遍历结构:
1
| [ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]
|
中序遍历结构:
1
| [ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]
|
递归:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
HashMap<Integer, Integer> map = new HashMap<>();
public TreeNode buildTree(int[] preorder, int[] inorder) {
int n = inorder.length;
for(int i=0; i<inorder.length; i++){
map.put(inorder[i], i);
}
return splitBuildTree(preorder, inorder, 0, n-1, 0, n-1);
}
public TreeNode splitBuildTree(int[] pre, int[] in, int lp, int rp, int li, int ri){
if(lp > rp) return null;
int pre_root = lp;
int in_root = map.get(pre[lp]);
TreeNode root = new TreeNode(pre[lp]);
int leftNum = in_root-li;
root.left = splitBuildTree(pre, in, lp+1, lp+leftNum, li, in_root-1);
root.right = splitBuildTree(pre, in, lp+1+leftNum, rp, in_root+1, ri);
return root;
}
}
|
437. 路径总和 Ⅲ
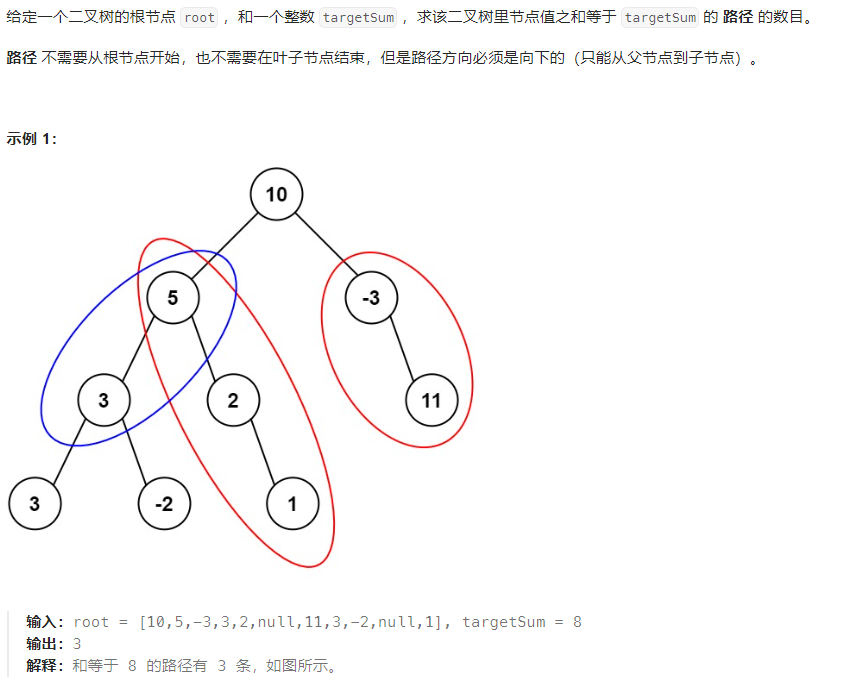
最简单的思路就是穷举法,以每一个结点为根,遍历所有可能的路径,如果满足就计数+1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public int pathSum(TreeNode root, long targetSum) {
if (root == null)
return 0;
int ans = rootSum(root, targetSum);
ans += pathSum(root.left, targetSum);
ans += pathSum(root.right, targetSum);
return ans;
}
public int rootSum(TreeNode root, long targetSum) {
if (root == null)
return 0;
int ret = 0;
if (root.val == targetSum) {
++ret;
}
ret += rootSum(root.left, targetSum - root.val);
ret += rootSum(root.right, targetSum - root.val);
return ret;
}
}
|
前缀和
通过 map 记录从根节点开始到每个结点的和,只要在前面结点中能够找到一个结点 pre[i] 到当前结点 pre[j] 的路径和为 targetSum,问题就解决了。
省去了第二层遍历,因为所有的路径都被“记住”了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
Map<Long, Integer> prefix = new HashMap<>();
public int pathSum(TreeNode root, long targetSum) {
prefix.put(0L, 1);
return dfs(root, 0L, targetSum);
}
public int dfs(TreeNode root, long cur, long targetSum){
if(root == null) return 0;
int ret = 0;
cur += root.val;
ret = prefix.getOrDefault(cur-targetSum, 0);
prefix.put(cur, prefix.getOrDefault(cur, 0)+1);
ret += dfs(root.left, cur, targetSum);
ret += dfs(root.right, cur, targetSum);
prefix.put(cur, prefix.getOrDefault(cur, 0)-1);
return ret;
}
}
|
236. 二叉树的最近公共祖先

哈希回溯定位
可以先遍历整个树,通过哈希表存储所有结点的父节点,这样就可以得到 p,q 的“继承”路线。
然后先回溯 p 的路线,并记录所有已访问的结点。
再回溯 q 的路线,同时匹配是否已访问,因为是自底向上,第一个存在的就是最近公共祖先。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution {
HashMap<TreeNode, TreeNode> parent = new HashMap<>();
HashSet<TreeNode> visited = new HashSet<>();
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
dfs(root);
while(p != null){
visited.add(p);
p = parent.get(p);
}
while(q != null){
if(visited.contains(q)){
return q;
}
q = parent.get(q);
}
return null;
}
public void dfs(TreeNode root){
if(root.left != null){
parent.put(root.left, root);
dfs(root.left);
}
if(root.right != null){
parent.put(root.right, root);
dfs(root.right);
}
}
}
|
标记回溯
最近公共祖先存在两种类型
1
2
3
4
5
6
7
8
| 分散在两边
0
/ \
p q
一方作为另一方的父结点
p
/ \
q
|
第一种情况,可以用两个标记变量表示
left: 表示左边存在一个 p / q
right: 表示右边存在一个 q / p
p 在左或在右都一样,第一种情况另一个一定在另一边。
所以当满足 left && right 此根节点就是 p,q 的祖先。
第二种情况类似,只需要额外判断自身是不是 p / q。
满足条件:(x == p || x == q) && (left || right) 即本身存在一个和左右存在一个。
再配合上递归回溯的特性,第一个满足的就是最近的祖先。
是否会存在这个 true 使得祖先不满足最近的特点?
不会,因为如果已经在一个子树确定了结果,另一个子树是不可能为 true 的,也就是祖先不会上升。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
TreeNode ans;
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
dfs(root, p, q);
return ans;
}
public boolean dfs(TreeNode root, TreeNode p, TreeNode q){
if(root == null){
return false;
}
int val = root.val;
boolean left = dfs(root.left, p, q);
boolean right = dfs(root.right, p, q);
if((left && right) || ((root == p || root == q) && (left || right))){
ans = root;
}
return left || right || (root == p || root == q);
}
}
|





