Apong's Blog

当你快坚持不住的时候，困难也快坚持不住了

0%

排序算法总结

发表于 分类于
记录了七大比较排序的代码实现和对比分析。

各大排序算法比较

排序算法 时间复杂度（平均） 时间复杂度（最差） 时间复杂度（最好） 空间复杂度 排序方式 稳定性
冒泡排序 O(n^2^) O(n^2^) O(n) O(1) 比较排序 稳定
选择排序 O(n^2^) O(n^2^) O(n^2^) O(1) 比较排序 不稳定
插入排序 O(n^2^) O(n^2^) O(n) O(1) 比较排序 稳定
希尔排序 O(nlogn) O(n^2^) O(nlogn) O(1) 比较排序 不稳定
归并排序 O(nlogn) O(nlogn) O(nlogn) O(n) 比较排序 稳定
快速排序 O(nlogn) O(n^2^) O(nlogn) O(logn) 比较排序 不稳定
堆排序 O(nlogn) O(nlogn) O(nlogn) O(1) 比较排序 不稳定

术语解释：

内部排序：所有排序操作都在内存中完成，不需要额外的磁盘或其他存储设备的辅助。这适用于数据量小到足以完全加载到内存中的情况。

外部排序：当数据量过大，不可能全部加载到内存中时使用。外部排序通常涉及到数据的分区处理，部分数据被暂时存储在外部磁盘等存储设备上。

稳定：如果 A 原本在 B 前面，而 A=B，排序之后 A 仍然在 B 的前面。

不稳定：如果 A 原本在 B 的前面，而 A=B，排序之后 A 可能会出现在 B 的后面。

是否稳定决定于，相同的元素在排序后是否还能保持原有位置。

排序分类

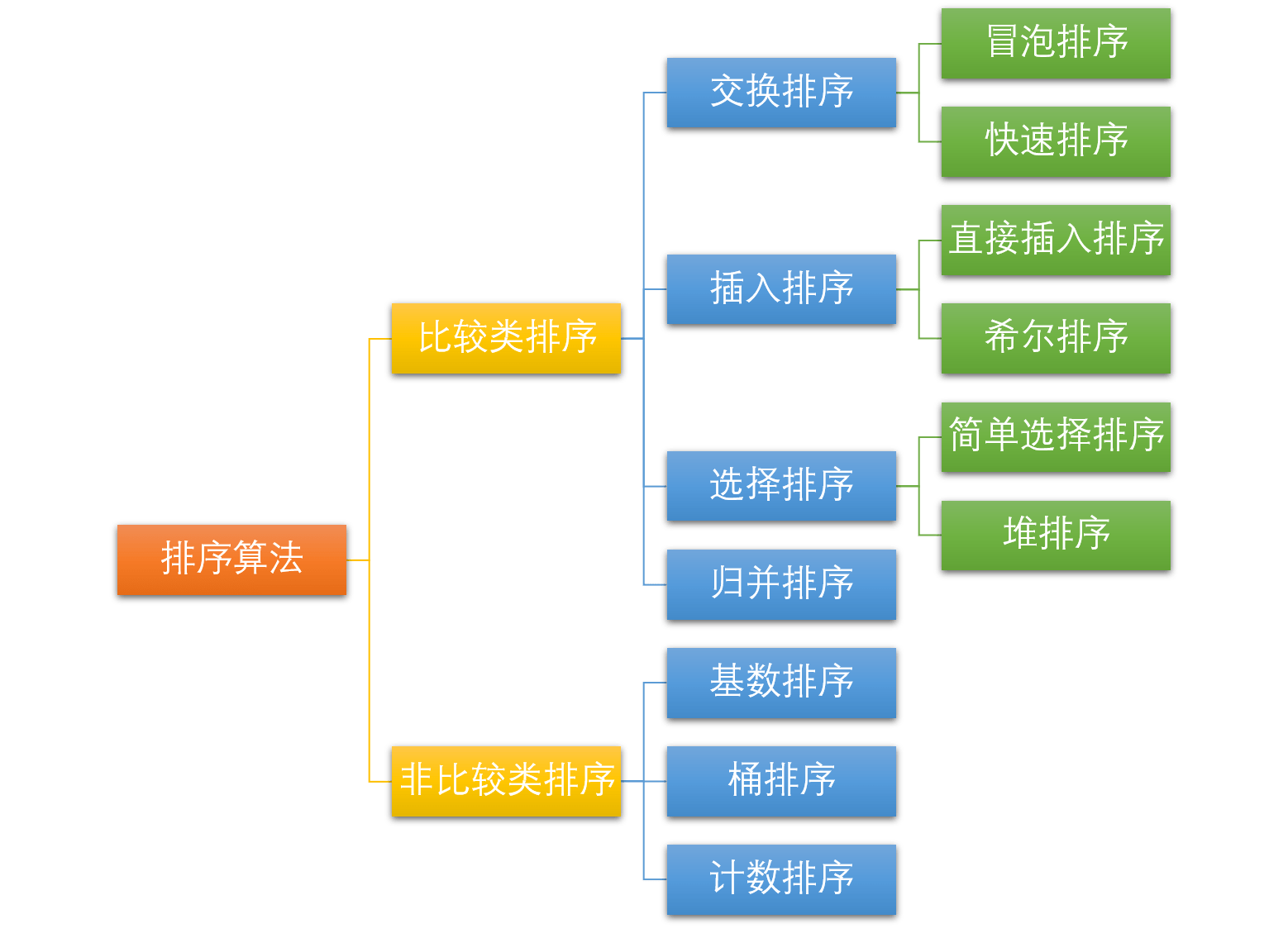
排序算法分类

比较类又被称为非线性时间排序，因为时间无法突破O(nlogn)

非比较类排序又被称为线性时间排序，可以达到O(n)

冒泡排序

重复遍历要排序序列，依次比较两个元素，一层一层往顶端方向缩短，越小的元素逐渐“浮”到尾端。

算法步骤

  1. 比较相邻的元素。如果第一个比第二个大，就交换它们两个；

  2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；

  3. 然后向头部缩短一个位置，即排除当次遍历区间的最后一个数（已经确定）；

  4. 重复步骤 1~3，直到排序完成。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * 冒泡排序
 * @param arr
 * @return arr
 */
public static int[] bubbleSort(int[] arr) {
    // 从 1 开始，因为是往后预知一位来比较
    for (int i = 1; i < arr.length; i++) {
        // 设置一个标志，用来确定当次遍历是否已经有序
        boolean flag = true;
        for (int j = 0; j < arr.length - i; j++) {
            if (arr[j] > arr[j + 1]) {
                int tmp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = tmp;
                // 出现乱序
                flag = false;
            }
        }
        // 如果已经有序，就退出排序
        if (flag) {
            break;
        }
    }
    return arr;
}

通过设置 flag ，可以使得最好时间达到 O(n)。

选择排序

首先在未排序序列中找到最小的元素，然后放到开头，

再继续从剩下的序列中找到最小的元素，放到开头的下一个，

如此重复。

算法步骤

  1. 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
  2. 再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
  3. 重复第 2 步，直到所有元素均排序完毕。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * 选择排序
 * @param arr
 * @return arr
 */
public static int[] selectionSort(int[] arr) {
    for (int i = 0; i < arr.length - 1; i++) {
        // 记录最小元素的索引
        int minIndex = i;
        for (int j = i + 1; j < arr.length; j++) {
            if (arr[j] < arr[minIndex]) {
                minIndex = j;
            }
        }
        // 排除自己
        if (minIndex != i) {
            int tmp = arr[i];
            arr[i] = arr[minIndex];
            arr[minIndex] = tmp;
        }
    }
    return arr;
}

为什么说选择排序不稳定？

以 [3a,7,6,5,3b,2] 为例：

当第一层找到最小元素 2 时，因为3a = 3b，本应该 3a 应该在前面，却被换到了 3b 后面。

插入排序

以第一个元素为基准，类似于扑克牌排序，将后面的数往大小往前面插入，当插好最后一张牌的时候就排好序了

算法步骤：

  1. 从第一个元素开始，该元素可以认为已经被排序；

  2. 取出下一个元素，在已经排序的元素序列中从后向前扫描；

  3. 如果该元素（已排序）大于新元素，将该元素移到下一位置，目的是空出位置；

  4. 重复步骤 3，直到找到已排序的元素小于或者等于新元素的位置；

  5. 将新元素插入到该位置后；

  6. 重复步骤 2~5。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * 插入排序
 * @param arr
 * @return arr
 */
public static int[] insertionSort(int[] arr) {
    // 从 1 开始，以第 0 个元素为基准
    for (int i = 1; i < arr.length; i++) {
        // 从已排序序列的最后一个开始
        int preIndex = i - 1;
        // 保留当前元素，防止位置被覆盖找不到
        int current = arr[i];
        while (preIndex >= 0 && current < arr[preIndex]) {
            // 如果扫描到的元素更大，就往后移
            arr[preIndex + 1] = arr[preIndex];
            preIndex -= 1;
        }
        // 遇到小于或等于的元素，直接插入到后一个位置。
        arr[preIndex + 1] = current;
    }
    return arr;
}

最好时间为：O(n)，当有序的时候，无需向前扫描。

希尔排序

其实就是给插入排序做了一个“预处理”。

将一个完整的序列分为 n 个增量间隔子序列，分别进行插入排序，最后增量变为 1，重新形成一个完整的序列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * 希尔排序
 *
 * @param arr
 * @return arr
 */
public static int[] shellSort(int[] arr) {
    int n = arr.length;
    int gap = n / 3;
    while (gap > 0) {
        for (int i = gap; i < n; i++) {
            int current = arr[i];
            int preIndex = i - gap;
            // Insertion sort
            while (preIndex >= 0 && arr[preIndex] > current) {
                arr[preIndex + gap] = arr[preIndex];
                preIndex -= gap;
            }
            arr[preIndex + gap] = current;

        }
        gap /= 3;
    }
    return arr;
}

不稳定：相同的元素会破坏顺序

归并排序

将序列不断分为两半，直到单位为 1 时开始回溯，将子序列进行有序合并，最后形成一个完整的有序序列。

为保证有序合并，需单独创建一个 O(logn) 的空间。

算法步骤：

  1. 如果输入内只有一个元素，则直接返回，否则将序列一分为二；

  2. 分别对这两个子序列进行归并排序，使子序列变为有序状态；

  3. 设定两个指针，分别指向两个已经排序子序列的起始位置；

  4. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间（用于存放排序结果），并移动指针到下一位置；

  5. 重复步骤 3 ~ 4 直到某一指针达到序列尾；

  6. 将另一序列剩下的所有元素直接复制到合并序列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
/**
 * 归并排序
 *
 * @param arr
 * @return arr
 */
public static int[] mergeSort(int[] arr) {
    if (arr.length <= 1) {
        return arr;
    }
    int middle = arr.length / 2;
    int[] arr_1 = Arrays.copyOfRange(arr, 0, middle);
    int[] arr_2 = Arrays.copyOfRange(arr, middle, arr.length);
    // 分治，回溯时完成排序
    return merge(mergeSort(arr_1), mergeSort(arr_2));
}

/**
 * 合并两个数组
 *
 * @param arr_1
 * @param arr_2
 * @return sorted_arr
 */
public static int[] merge(int[] arr_1, int[] arr_2) {
    // 创建一个能够容纳两个数组合并后所有元素的空间
    int[] sorted_arr = new int[arr_1.length + arr_2.length];
    int idx = 0, idx_1 = 0, idx_2 = 0;
    // 有序合并
    while (idx_1 < arr_1.length && idx_2 < arr_2.length) {
        // 由于arr1属于左半边，arr2属于右半边，如果相同应保证左边元素先加入
        if (arr_1[idx_1] <= arr_2[idx_2]) {
            sorted_arr[idx] = arr_1[idx_1];
            idx_1 += 1;
        } else {
            sorted_arr[idx] = arr_2[idx_2];
            idx_2 += 1;
        }
        idx += 1;
    }
    // 数组1还有元素
    if (idx_1 < arr_1.length) {
        while (idx_1 < arr_1.length) {
            sorted_arr[idx] = arr_1[idx_1];
            idx_1 += 1;
            idx += 1;
        }
    } else {
        // 数组2还有元素
        while (idx_2 < arr_2.length) {
            sorted_arr[idx] = arr_2[idx_2];
            idx_2 += 1;
            idx += 1;
        }
    }
    // 返回本次归并的有序序列。
    return sorted_arr;
}

快速排序

和归并排序相似，区别是在分治的同时进行分区，

而前者是在回溯的时候借助额外空间返回有序序列。

先选定一个基准，根据基准分隔成两个部分（分区1 < 分区2），然后在基准的位置分裂进行分区。

只要保证每次分区左边的小于右边的，那么当分裂到 1 个时就排好序了。

算法步骤：

  1. 从序列中随机挑出一个元素，做为 “基准”(pivot)；

  2. 改变序列分布，将所有比基准值小的元素摆放在基准前面，所有比基准值大的摆在基准的后面（相同的数可以到任一边）。

  3. 操作结束之后，该基准就分割了两片区域（分区1 < 分区2）。

  4. 分别对两片区域继续进行递归分区。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public static int partition(int[] array, int low, int high) {
    // 默认以尾部为基准
    int pivot = array[high];
    // 从开头开始
    int pointer = low;
    for (int i = low; i < high; i++) {
        // 只要小于等于基准值的就移动到前半部分
        if (array[i] <= pivot) {
            int temp = array[i];
            array[i] = array[pointer];
            array[pointer] = temp;
            pointer++;
        }
        System.out.println(Arrays.toString(array));
    }
    // 此时 pointer 为基准的分区位置，交换基准值过来
    // 如果默认选取中间值为基准，则无需移动。
    int temp = array[pointer];
    array[pointer] = array[high];
    array[high] = temp;
    return pointer;
}
public static void quickSort(int[] array, int low, int high) {
    if (low < high) {
        // 先分区再分治
        int position = partition(array, low, high);
        quickSort(array, low, position - 1);
        quickSort(array, position + 1, high);
    }
}

最坏时间原因：当每次分治选取的基准值都是极值（max or min）时，时间等同于O(n^2^)

不稳定的原因：无相对位置的交换

  1. 分区元素交换
  2. 基准值位置交换

可能存在比基准值大的数，被交换到了尾部

如：[1,2,3,4,6a,7,8,6b,5]

在确定了左半区（<=5）时，需要移动 5 到分区位置，此时 6a 被交换到了原先 5 的位置

[1,2,3,4,5,7,8,6b,6a]

堆排序

关键在于建立大顶堆，将顶部和最后一个元素交换，再重新堆化，重复取出最大元素放在尾部，直到只剩一个元素即排序完成。

  1. 将初始待排序列 (R1,R2,…,Rn) 构建成大顶堆，此堆为初始的无序区；

  2. 将堆顶元素 R1 与最后一个元素 Rn 交换，此时得到新的无序区 (R1,R2,…,Rn−1) 和新的有序区 Rn, 且满足 Ri⩽Rn(i∈1,2,…,n−1)；

  3. 由于交换后新的堆顶 R1 可能违反堆的性质，因此需要对当前无序区 (R1,R2,…,Rn−1) 调整为新堆，然后再次将 R1 与无序区最后一个元素交换，得到新的无序区 (R1,R2,…,Rn−2) 和新的有序区 (Rn−1,Rn)。不断重复此过程直到有序区的元素个数为 n−1，则整个排序过程完成。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
/**
 * 交换
 * @param arr
 * @param i
 * @param j
 */
private static void swap(int[] arr, int i, int j) {
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
}

/**
 * 构建大顶堆
 * @param arr
 */
private static void buildMaxHeap(int[] arr) {
    // 从最后一个非叶子结点开始，由底向上选举最大值。
    // 如果从上往下，无法确定顶部和隔层哪个更大，应该从底部一层一层往上。
    for (int i = arr.length / 2 - 1; i >= 0; i--) {
        heapify(arr, i);
    }
}

/**
 * 堆化
 * @param arr
 * @param i
 */
private static void heapify(int[] arr, int i, int heapLen) {
    int left = 2 * i + 1;
    int right = 2 * i + 2;
    // 选取最大值，构建大顶堆
    int largest = i;
    if (right < heapLen && arr[right] > arr[largest]) {
        largest = right;
    }
    if (left < heapLen && arr[left] > arr[largest]) {
        largest = left;
    }
    if (largest != i) {
        swap(arr, largest, i);
        // 逐层选举最大值
        heapify(arr, largest);
    }
}

/**
 * 堆排序
 * @param arr
 * @return
 */
public static int[] heapSort(int[] arr) {
    // 堆的线性长度
    int heapLen = arr.length;
    // 构建大顶堆
    buildMaxHeap(arr);
    for (int i = arr.length - 1; i > 0; i--) {
        // 逐一移动最大到数组尾部
        swap(arr, 0, i);
        // 缩减堆空间，重新从顶向下堆化
        heapLen -= 1;
        heapify(arr, 0, heapLen);
    }
    return arr;
}

不稳定：因为在构建堆的时候比较最大值和相对位置无关，并且还有可能分在了不同子树上